Thinking in Stories: A Mathematical Perspective

Texture AI’s work is strongly grounded in the academic work of its members. James Carney and Cole Robertson, in particular, have worked on many projects and articles together. Once such article is Fictional narratives as variational Bayesian method for estimating social dispositions in large groups, which they published with Oxford collaborator Tamás Dávid-Barrett in the Journal of Mathematical Psychology.
This article applies ideas from machine learning and Bayesian inference to one of the oldest human practices––namely, storytelling. Its aim is to show that these very abstract ideas can be used to explain why human beings in all cultures tell stories that exhibit the same roles and structures, despite most other forms of culture showing substantial variation. When this happens, it often means that the cultural form in question has a basis in an underlying cognitive mechanism.
James, Cole, and Tamás argue that storytelling is rooted in cognitive processes designed to make it easier to track social dispositions in large groups. There is some evidence that human beings are mentally equipped to deal with groups of approximately 150 people. However, the actual group sizes in which human beings exist have been steadily increasing since the Palaeolithic––with modern cities typically containing several million people. This means that there is a mismatch between the social reality we are equipped to deal with the social reality we are required to deal with. How do we bridge the gap?
This is where storytelling enters the picture. Researchers on narrative long ago noticed that even when the number of characters in a story is large, the number of roles they play is relatively small: one theory suggests that all every role in a narrative is associated with wanting something (desire), aiding or impeding an agent who wants something (alliance), or legitimating or benefitting from an agent wanting something (legitimacy). Crucially, however, while these roles are simple enough to fall within human social processing abilities, they are sophisticated enough to capture many forms of social life. In this sense, stories optimally balance computational load against predictive accuracy.
Building on previous work by Tamás and James, James, Cole, and Tamás show that this account of storytelling can be represented as a form of modelling known as variational Bayesian inference (VBI). What VBI methods show is that we can estimate unknown variables in a conditional probability distribution by minimising the difference between the unknown distribution and a known distribution. For example, it can be seen from Figure 1 that the distribution Q(Z) in the bottom panel offers a better representation of P(Z|X) than does Q(Z) in the top panel.
Viewed through this lens, the recurring roles in storytelling define a probability distribution that we can use to estimate the ‘true’ probabilities of the social realities we encounter in everyday life. If James, Cole, and Tamas’s model is correct, it predicts that the more familiar we are with a given social reality, the less we will need to create stories about it; reciprocally, unknown social realities should prompt sustained attempts at sense-making through narrative.
So far, these predictions have only been tested via simulation, where they seem to stack up. But more research is needed before this model of storytelling can be endorsed as a plausible account of how humans actually think.
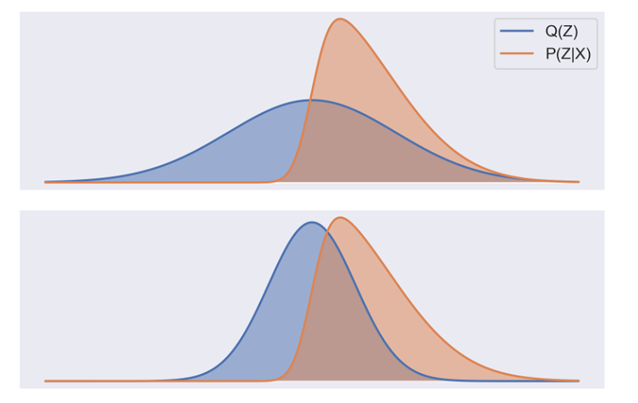
Figure 1: Estimation of an unknown probability distribution, P(Z|X), by way of a known distribution, Q(Z).

